Pinealog

the first analog watchface to be introduced into Infinitime. this watchface is the epitome of elegance

for Infinitime (latest - 0.14)

Source code:

can be found here

pre-compiled Infinitime:

download here

documentation:

This watchface is the base example for many of my other analog watchfaces due to the technique in which it has been made possible the reason this watchface took a while to come up with was because of the limitation of the graphics library in Infinitime which is LVGL, specifically v6.x of the library which has the problem.

the original technique to emulate an analog watchface was with a function called lv_img_set_angle which would have been used to rotate an image that looked like a clock hand, in an angle with respect to time. ie. seconds 0 to 60 (multiply by 6 to get 0 to 360, covering the entire range of angles)

eg. if no of seconds is 25, 25 x 6 = 150 degrees is the angle the seconds hand would point to..

minutes 0 to 60 (multiply by 6 to get 0 to 360, covering the entire range of angles)

eg. if no of minutes is 31, 31 x 6 = 186 degrees is the angle the minutes hand would point to..

hours 0 to 24, but with hours its a little different, when the time was within 0 to 12 multiply by 30 to get 0 to 360, and when it was past 12, subtract 12 to get the hours past noon covering the entire range of angles

eg. if the hour was 7 or 7AM, 7 x 30 = 210 degrees but. eg. if the hour was 15 or 3PM, (15 - 12) x 30 = 3 x 30 = 90 degrees is the angle it would be pointing to..

simple right ? but the problem is that, lv_img_set_angle is a feature that only exists in the latest version of LVGL v7 library. so how do we get around this ?

but using something called lv_line we can set a line from two points or even more points, by giving it an Array of coordinates. simple usage, but you can use this for this our complex need, by making this act as the clock hand, which points at the angle representing time.. but lv_line isn’t set by an angle. as said before you have to specify points, since we need one line, we need two points.

we know that the clock hand originates from the center of the watchface.

but where is the other point !? 🤔

well we know that the clock hand moves around in a circle, and so here we need to look at some simple trignometry.

from basic trignometry we know

sin θ = length of the opposite side from the angle / length of the hypothenuse cos θ = length of the adjacent side of the angle / length of the hypothenuse

here the hypothenuse is the length of the the clock hand, and θ is the angle of the arm

ref. to this image below.

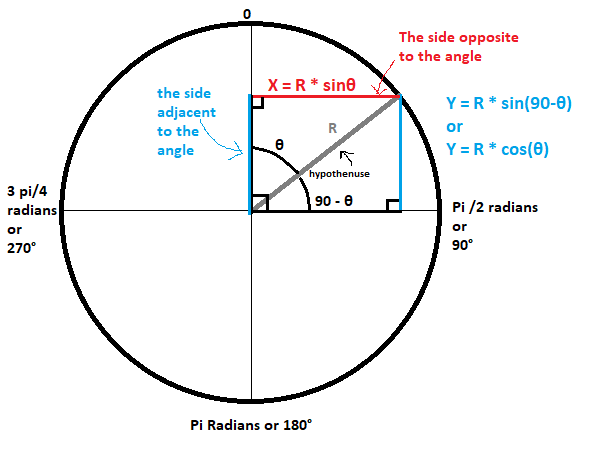
sin θ = X/R sin(90 - θ) = cos θ = Y/R

pushing the variables to the other side, we get, X = R * sin θ Y = R * cos θ

hence to get the the other X and the Y coordinates of the second point of the line, we can use this basic trignometric concept.

in code this is what happens within the Clock::Refresh() function

if(hour <= 12){
    hour_angle = hour * 30;
  }
else if(hour > 12){
    hour_angle = (hour - 12) * 30;
  }
      
minute_angle = minute * 6;
    
second_angle = second * 6;
    
hour_sin = sin(hour_angle * 0.017);
hour_cos = cos(hour_angle * 0.017);

minute_sin = sin(minute_angle * 0.017);
minute_cos = cos(minute_angle * 0.017);

second_sin = sin(second_angle * 0.017);
second_cos = cos(second_angle * 0.017);

hour_x = 120 + floor(hour_sin*hour_len);
hour_y = 120 - floor(hour_cos*hour_len);

minute_x = 120 + floor(minute_sin*minute_len);
minute_y = 120 - floor(minute_cos*minute_len);

second_x = 120 + floor(second_sin*second_len);
second_y = 120 - floor(second_cos*second_len);

hour_points[1] = {const_cast<int&>(hour_x),  const_cast<int&>(hour_y)};
minute_points[1] = {const_cast<int&>(minute_x),  const_cast<int&>(minute_y)};
second_points[1] = {const_cast<int&>(second_x),  const_cast<int&>(second_y)};
    
lv_line_set_points(hour_hand, hour_points, 2);
lv_line_set_points(minute_hand, minute_points, 2);
lv_line_set_points(second_hand, second_points, 2);

lets break it up to see which does what.

1. assigning the value of the angle

if(hour <= 12){
    hour_angle = hour * 30;
  }
else if(hour > 12){
    hour_angle = (hour - 12) * 30;
  }
      
minute_angle = minute * 6;
    
second_angle = second * 6;

this is the part which gets the value of the angle. hour, minute, and second are the variables which have the value of time in their respective names. and hour_ angle, minute_angle, and second_angle are the respective variables to which the angle is assigned.

2. getting the values of the trignometric constants

hour_sin = sin(hour_angle * 0.017);
hour_cos = cos(hour_angle * 0.017);

minute_sin = sin(minute_angle * 0.017);
minute_cos = cos(minute_angle * 0.017);

second_sin = sin(second_angle * 0.017);
second_cos = cos(second_angle * 0.017);

this part get the trignometric constants, i.e the “sin θ” value sin(), cos() are functions which belong to the native C++ math library. it is used with #include <math.h>

if seen closely, it is multiplied with 0.017, this is because the sin(), cos() function will only accept the angle in “radians” hence to convert degrees to radians, we multiply it with pi/180 or 3.14/180 which is equal to 0.017

3. getting the x and y coordinates

hour_x = 120 + floor(hour_sin*hour_len);
hour_y = 120 - floor(hour_cos*hour_len);

minute_x = 120 + floor(minute_sin*minute_len);
minute_y = 120 - floor(minute_cos*minute_len);

second_x = 120 + floor(second_sin*second_len);
second_y = 120 - floor(second_cos*second_len);

this part of the code is responsible for getting the x and y coordinates. eg. hour_sin * hour_len gives us the x coordinate

but why are we using floor function, and why add and subtract 120 ?? let’s elaborate.

we need to get the exact coordinate (an integer, and a whole number value from 0 to 240) and that coordinate represents a particular pixel on the screen, and since there is no such thing as “half a pixel” or “a fraction of a pixel” we need to round it off, the floor() function is another part of the math library. it rounds off the given number converting it from float (floating point value) or double (double precision floating point value) to an int (integer), specifically the closest smallest integer value.

eg. 98.67 to 98, or 99.99 to just 99, it always brings it to the lowest closest value for negative numbers, this would mean -1.34 to -2, or -0.01 to -1.

hence that solves the reason for why the floor function is used,

but why 120 ? if you take a look at the way LVGL works and how coordinates are mapped. the cartesian origin of the screen is the top left corner, and going down is considered having a positve Y value (inverse of the normal Y coordinate) and going to the right is considered having a positve X value (normal X coordinate).

and since we are at the center, which is (120, 120), we need to take into account the offset from that origin, but why 120 + for the X coordinate, and 120 - for the Y coordinate ? since the y coordinate is inverted, we have to consider going up as having a negative Y value.

hence its subtracted by the found Y coordinate.

4. assigning the coordinate values to the array.

hour_points[1] = {const_cast<int&>(hour_x),  const_cast<int&>(hour_y)};
minute_points[1] = {const_cast<int&>(minute_x),  const_cast<int&>(minute_y)};
second_points[1] = {const_cast<int&>(second_x),  const_cast<int&>(second_y)};

these lines, assign the coordinates to the array. hour_points is the array containing the coordinates, its like, hour_points[] = { {120, 120}, {hour_x, hour_y} };

but since we are only changing the second coordinate, we cast the value to its index by, hour_points[1] = {const_cast<int&>(hour_x), const_cast<int&>(hour_y)};

the function const_cast<int&>() is used to type cast the double value previously obtained from the X coordinate hour_x = 120 + floor(hour_sin*hour_len);

to an integer variable. it is able to convert the type because we have the value in int form (after using the floor() function) and the const_cast gives the variable const-ness or the have the ability to act like a mutable constant.

5. setting the points in lv_line_set_points

lv_line_set_points(hour_hand, hour_points, 2);
lv_line_set_points(minute_hand, minute_points, 2);
lv_line_set_points(second_hand, second_points, 2);

these lines set the points of the line, its syntax is, lv_line_set_points(<line pointer>, <pointer to the array with the points> , <number of points>);

and with that it magically shows analog time with the use of lv_line widget. you can find more intricate documentation at LVGL docs